

 The
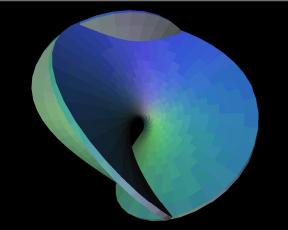
Gauss Map
of a surface associates to each
The
Gauss Map
of a surface associates to each
In these studies, the Unit Normals
to the surface are used to create
a color mapping on the surface
which imitates the default
Mathematica
(lighting)/rendering model.
LightSources
{{{1.,0.,1.},RGBColor[1,0,0]},{{1.,1.,1.},
RGBColor[0,1,0]},{{0.,1.,1.},RGBColor[0,0,1]}}
In these studies, however, the color calculations are done in CMY color space and the background is white.
Stewart Dickson has written the software to convert the Gauss-map of an object to a Mathematica-style surface color map. Download here.
The texture image is parametrically
mapped along the knotted torus.
Color 3-D Printing was done by Z Corporation. Download here.


A snail shell generated in Mathematica Download here.
 The Seventeenth-Century French mathematician Pierre de Fermat wrote in the
margin of his copy of Arithmetica by Diophantus, near the section
on the Pythagorean Theorem (a squared plus b squared equals c squared),
The Seventeenth-Century French mathematician Pierre de Fermat wrote in the
margin of his copy of Arithmetica by Diophantus, near the section
on the Pythagorean Theorem (a squared plus b squared equals c squared),
"x ^ n + y ^ n = z ^ n - it cannot be solved with non-zero integers x, y, z for any exponent n greater than 2. I have found a truly marvelous proof, which this margin is too small to contain."This was left as an enigmatic riddle after Fermat's death and it became a famous, unsolved problem of number theory for over 350 years.
Andrew Hanson has made some pictures, and I have in turn made sculpture, of a system analogous to Fermat's last theorem - a superquadric surface parameterized in complex four-space.
We think that the mathematics of the n=3 case are similar to Fermat's own proof of the n=3 special case. Our pictures have lent some visual concreteness to the recent news of Andrew Wiles' proof of the Taniyama-Weil conjecture, which implies the proof of Fermat.
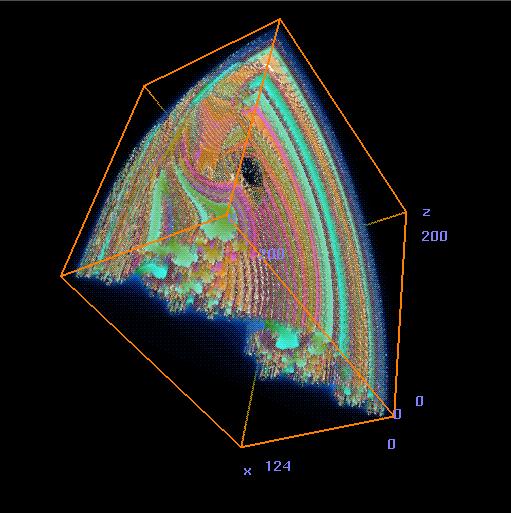 The
Z Corporation
3-D Color Printer has a
Bit-Mapped, color image slice-based software interface to its
build process. This interface
makes the
Z Corp
machine the ideal platform on which to execute the
Fractal Zoom in Three Physical Dimensions -- and in color!
The
Z Corporation
3-D Color Printer has a
Bit-Mapped, color image slice-based software interface to its
build process. This interface
makes the
Z Corp
machine the ideal platform on which to execute the
Fractal Zoom in Three Physical Dimensions -- and in color!
Stewart Dickson has written the software to interface this data object to the Z Corp 3-D Color Printer. Download here.

 The artist has developed the
The artist has developed the
This file format is suitable
for output using the
Z Corp
Color 3-D Printer. Download here.
 "Botty Shelly"
"Botty Shelly"


Stewart Dickson, Sculptor 110 N. Whipple St. Fort Bragg, CA 95437 USA (707)813-0385 MathArtSPD@gmail.com