This work began in 1993 using software by the author, free software available over the Internet, and computer hardware belonging to the author's employer at the time, The Post Group, Hollywood.

This work continues today, with the advent of the Z Corporation 3-D Color Printer

In November, 1993, students at the Department of Mechanical Engineering, University of Texas at Austin, under the direction of Professor Richard Crawford were able to produce the first sculpture of a true, 3-D deterministic fractal, constructed particle-by-particle from a pixel-volume database using a Selective Laser Sintering (SLS) machine.

Figure 1.

This sculpture is a physical reproduction of the convergence potential plot of the iterative procedure Z -> e^(i theta) Z^2 + e^(-i theta) C, where Z is a complex quaternion four-vector of the form (a, b i, c j, d k), C is the Quaternion constant value (0.2809,-0.53,0.0,0.0) and theta is an angle of rotation in the complex plane equal to pi/2.

The resolution of the Julia set pictured here is 400 by 400 by 200, at 0.01 inch per volume particle -- the finest particle resolvable by the student-built SLS device at UT Austin. The overall dimensions of the sculpture are 4 inches by 3 inches by 2 inches. The maximum build capacity of the UT-Austin research SLS machine was 4 inches by 4 inches by 4 inches.

It is the author's belief that this sculpture is the first of its kind to come into existence, because the student-built SLS machine at UT Austin has a custom software interface, designed by the students, which can support printing a 3-D model directly from a pixel volume. Most other commercial rapid-prototyping systems only support the polygon-based '.STL' object description format.

Figure 2.

This image is a computer-generated rendering of the pixel volume data used to construct the sculpture.

This document proposes doing the "Fractal Zoom" on the 3-D section of the Quaternion (complex 4-D) Julia Set in three physical dimensions. The following images depict the concept.

Figure 3.

This is the Mandelbrot set -- the two-dimensional graph of the convergence potential of the dynamical process Z -> Z x Z + C, where Z is initialized to (0, 0) on the first iteration and the convergence is plotted for the value C in the complex plane (x, i y) over the range (-2.25, -i 1.125), (0.75, i 1.125).

Figure 4.

This is the two-dimensional version of the Julia set -- a compliment graph to the Mandelbrot set -- computed for C equal to (-0.75, i 0.113), and Z initialized at each plotted point over the displayed range of the complex plane. This graph is also rotated 90 degress (pi/2 radians) about the origin in the complex plane.

Figure 5.

This is the Julia set computed in Quaternion Complex Four-Space for the point C = (-0.75, 0.113, 0.01, 0.01) plotted for Z initialized at points over the volume from (-1.5, -1.5, -1.5, 0.05) to (1.5, 1.5, 1.5, 0.05) in a cube sampled at 200 by 200 by 200 points. The non-trivial portion of the graph actual spans a pixel volume of only 200 by 200 by 148.

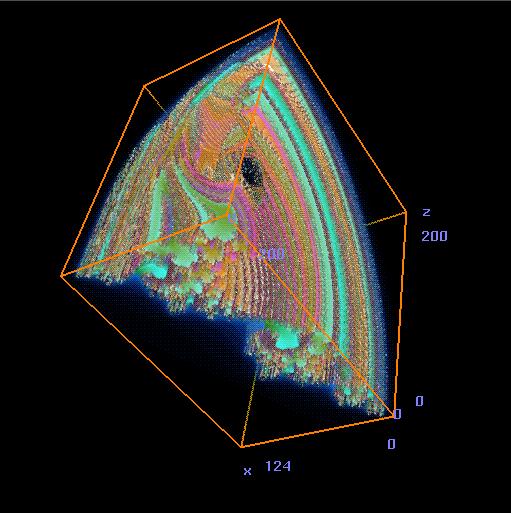
Figure 6.

This is one octant (one-quarter of half the plot, divided at the X-Y plane) of the Julia set shown in Figure 5, evaluated over Quaternion space from (0, 0, 0, 0.05) to (1.5, 1.5, 1.5, 0.05), "blown-up" again to a 200 by 200 by 200 cube. You can see a portion of the 2-D Julia set in cross-section in the X-Y plane (z = 0) on the bottom face of the cube.

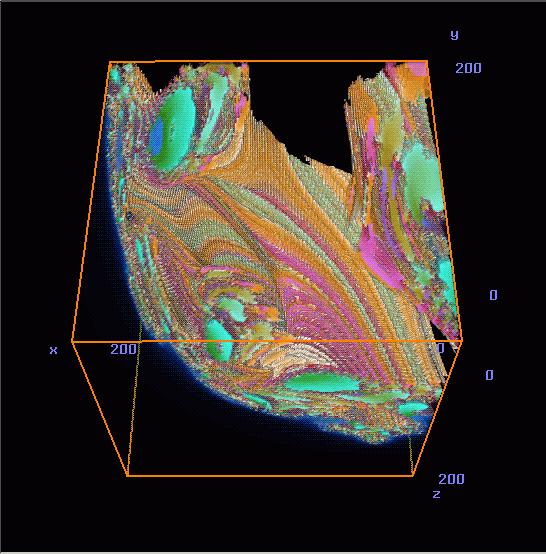
Figure 7.

This is an even smaller portion of the Julia set -- one-eighth of the portion shown in Figure 6, evaluated over Quaternion space from (0, 0, 0.75, 0.05) to (0.75, 0.75, 1.5, 0.05), again "blown-up" to the 200 by 200 by 200 cube.

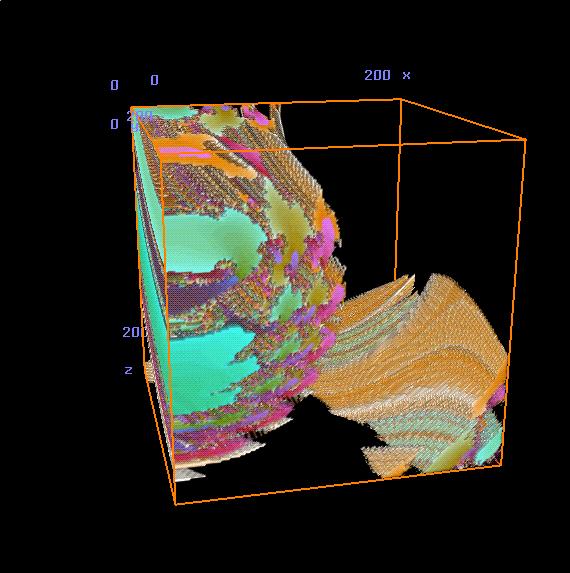
Figure 8.

This is a continuation -- one-eighth of Figure 7, again "blown-up" to 200 by 200 by 200.

The process is infinitely repeatable -- down to the numerical precision of the computer -- on an infinite number of Julia sets. There is a unique Julia set for every point on the Mandelbrot set.

DTM Corporation is the company, spun off by Professor Joseph Beaman, Department of Mechanical Engineering, U-T Austin, the original inventor of the SLS process. DTM Corporation manufactures the commercial/industrial version of the Selective Laser Sintering machine.

The author has been told that the Department of Mechanical Engineering, U-T has received an older, commercial-grade machine from DTM Corp. And it is the author's understanding that the students and staff there have modified its software to support building pixel volumes, such as the sculptures depicted here. This machine is said to be of higher mechanical precision than the student-built machine. It also has a cylindrical build envelope of 12 inches diameter by 14 inches deep and can resolve volume elements smaller than 0.01 inches.

The commercial SLS machine can build objects directly in Polycarbonate (thermoplastic, used in injection molding), casting wax, Zircon and Silica metal-casting mold materials. The author has investigated casting sculptures in anodized Titanium. It is proposed that reproductions of final output from this project be attempted in this medium as well.

To build larger than 4 inches by 4 inches by 4 inches requires a huge quantity of data to be transferred to the machine. The only feasible way to do this is to have the computer generating the sculpture physically connected to the Selective Laser Sintering Machine, feeding it data as it is generated.

Z Corporation, Burlington, MA has recently announced the Z402C 3D Color Printer, the world's first commercially available rapid prototyping device that can create physical parts in multiple colors.

The Z Corp Z402C 3D Color Printer has a color, bitmap image slice-based software interface. This is the ideal machine for executing this proposal.

The following are Z-Corp color 3D prints of the forward-solved convergence map of (16 iterations of) Z -> e^{i R} Z2 + e^-i R (0.2809,0.53,0.01,0.01), R -> (π/4) In Z-Corp's plaster-of-paris and super-glue. Dimensions are: 2.78"(H) X 4.78"(W) X 4.78"(D) It was rendered from a triangle isosurface mesh created in Kitware's Visualization ToolKit (Vtk) from a 1024³ x 8bit/voxel volume. The ASCII "OBJ" file was 1,626,027,010 bytes in size (330Mbytes gz-compressed) and had 19,428,506 triangles. The giga-voxel volume computed in 49min, 7.779sec (real); 3min, 28.106sec (user); 16min, 8.695sec (sys) using a parallel program running as three processes on a 2x2.4GHz Intel Core2Duo with 7.8GBytes of Ram running RedHat Fedora Core 9 x86_64.

The object was printed on a Z Corp Z 510 Color 3D Printer at the Visualization, Media and Imaging Laboratory (VMIL) of the Imaging Technology Group (ITG) Beckman Institute University of Illinois at Urbana-Champaign.

Builds by Z Corp Z 510 Color 3D Printer at the Visualization, Media and Imaging Laboratory (VMIL) of the Imaging Technology Group (ITG) Beckman Institute University of Illinois at Urbana-Champaign and on FormLabs by CKC1010

The author proposes building a unique kind of sculptor's studio, in order to continue this work.

The objects and images shown in this document were created using software created by the author, the Army High-Performance Computing Research Center "Brick O' Bytes (BOB)" interactive volume visualization software, Kitware's Visualization ToolKit (Vtk) and Maya.