From Webster's Revised Unabridged Dictionary (1913) (web1913), "Hypertext Webster Gateway at UCSD", <http://work.ucsd.edu:5141/cgi-bin/http_webster>:

Zoetrope \Zo"e*trope\, n. [Gr. ? life + ? turning, from ? to turn.] An optical toy, in which figures made to revolve on the inside of a cylinder, and viewed through slits in its circumference, appear like a single figure passing through a series of natural motions as if animated or mechanically moved.

In this zoetrope, sixty phases of the object which transforms are attached to the edge of a wheel. The rotation of the wheel is "frozen" using a stroboscopic light, optically synchronized to the "spokes" of the wheel where the objects project from its edge.

The proposed subject for this zoetrope is the homotopy or metamorphosis from a simple torus to Costa's Minimal Surface.

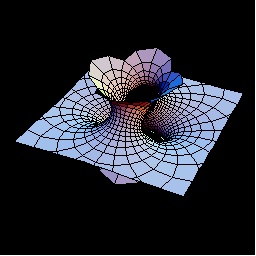
The figure is Costa's genus 1 three-ended minimal surface rendered in the Mathematica system for doing mathematics by computer.

Costa's Minimal Surface was the first example of an infinitely large class of minimal surfaces discovered by David Hoffman, WIlliam Meeks III and James Hoffman at the University of Massachusetts, Amherst between 1983 and 1985. The object was initially proposed by a graduate student named Celsoe Costa in Rio de Janeiro, but the mathematics were so complicated, they obscured the underlying geometry.

When David Hoffman began to make pictures (graphs) of aspects of Costa's mathematics, it became clear that the surface contained symmetry no-one had expected when looking at the mathematics alone. Hoffman and his team then modified the mathematics to generalize the surface based upon its periodic symmetry. This breakthrough in the mathematics of minimal surfaces (the previous major discovery in the field occurred in the late 1800's) was brought about by visual computing.

Costa's surface is also known as the Genus One, Three-Ended Minimal Surface of the Costa-Hoffman-Meeks family. The surface is obtained topologically by pulling a simple torus inside-out, opening it at three points. Looking at Costa's minimal surface by itself, it is not obvious how this is done. But, by looking at a computer-generated metamorphosis, it is immediately clear.

The artist finds 3-D computer graphics a tantalizing glimpse of a powerful way of interacting with abstraction. However, it is also highly frustrating in its inaccessibility in terms of physical experience. Since 1989 the artist has been using computer-aided rapid mechanical prototyping technologies, such as Stereolithography and Selective Laser Sintering to render artifacts from the historical legacy of CyberSpace in physical materials.

The present proposal is to demonstrate computer-generated metamorphosis of an object in three physical dimensions in real materials.

The artist proposes that the 3-D Zoetrope can be constructed at three different scales, using two different modeling methods.

The initial proposal can be constructed at a scale of approximately twenty inches in diameter and four inches in height from a single CAD model, as depicted in the accompanying animation. In this version, the wheel is integral to the object which metamorphoses.

The initial design proposes to economise on Rapid Prototyping building resources at the expense of the data volume of the CAD model -- the binary STL file occupies nearly twenty megabytes of data.

The proposed mechanical mounting scheme for the sculpture is depicted as follows:

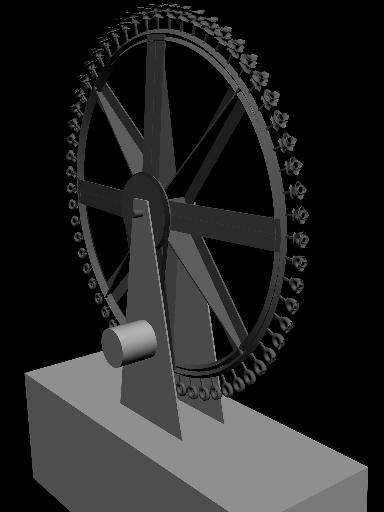
A larger version of the project can be constructed using a readymade wheel, such as a bicycle wheel, and a set of sixty objects (in turn composed of two copies of a set of thirty objects) attached to the edge of the wheel.

At this scale, thirty (half) of the computer-generated objects for the piece can be constructed at a time within a twelve-inch-square area approximately four inches high. Each object will include a standardized base, which will attach to the wheel and register the object in its spatial frame of reference as it "morphs".

The proposed museum presentation for the sculpture is as follows:

In this presentation, the rotating sculpture is effectively sealed within its pedestal, but is viewable from three sides.

Larger versions of the project can be constructed using a custom-made wheel and sixty computer-generated objects constructed individually or in groups of four, nine, sixteen, etc. depending on their size and the capacity of the machine used to build them.